Chapitres
Les ondes et leur fonctionnement
Avant de parler du phénomène des interférences et de comprendre son fonctionnement, il est important de faire quelques rappels sur les ondes, à l'origine du phénomène.
Une onde se propage dans toutes les directions qui lui sont offertes. L’onde se propage de proche en proche. Certaines ondes ont besoin d'un milieu matériel pour se transmettre. C'est le cas par exemple des ondes sonores qui seraient incapables de se propager dans le vide
Une onde est une déformation qui se propage dans un milieu, qu'il soit matériel ou non. Il existe deux types d'ondes : les ondes mécaniques et les ondes électromagnétiques.
Il existe deux types d'ondes : les ondes électromagnétiques et les ondes mécaniques.
Une onde mécanique est une onde qui se propage dans un milieu matériel avec un transfert d'énergie et ce sans transfert de matière.
En ce qui concerne l'onde électromagnétique, il s'agit d'une onde résultant d'une vibration entre un champ électrique et un champ magnétique qui peut alors se propager parmi les milieux matériels comme immatériels, le vide par exemple.
Une onde se définit principalement par l'une de ses caractéristiques : la longueur d'onde.
La longueur d’onde est une grandeur physique homogène à une longueur. Elle est caractéristique d'une onde monochromatique (composée d'une seule couleur). Dans un milieu homogène, elle définit la distance séparant deux maxima (c'est à dire, deux valeurs maximales) consécutifs de l'amplitude. Il est important de savoir que la longueur d'onde dépend de la célérité. Selon le milieu qu'elle traverse, cette dernière sera plus ou moins élevée.
Cependant, lorsque l'onde n'est pas monochromatique, il est possible d'effectuer une analyse harmonique pour la décomposer en une somme d'ondes monochromatiques. Il ne faut pas oublier que les phénomènes physiques ne sont jamais strictement périodiques : en effet, l'analyse spectrale aboutit en une somme infinie d'ondes monochromatiques. On considère alors la longueur d'onde dominante (c'est-à-dire celle qui correspond à la fréquence qui transporte le plus d'énergie) comme l'onde qui présente la fréquence centrale de la plage qui transporte le plus d'énergie. Les longueurs d'onde sont couramment utilisées en acoustique, en radio et en optique par exemple. Toute onde périodique (onde dont la perturbation se répète à intervalles réguliers) peut être caractérisée par une double périodicité :
- La périodicité temporelle, représentée par la période temporelle ;
- La périodicité spatiale, représentée par la longueur d'onde.
La longueur d'onde est la distance la plus courte qui sépare deux moments identiques de la perturbation.
La longueur d'onde est habituellement notée à l'aide de la lettre grecque lambda (λ). Dans le système usuel, on utilise souvent le nanomètre (nm) comme unité. Dans le système international (SI), elle se note en mètre (m).
Il existe un lien entre la période temporelle et la longueur d'onde. Ce dernier est défini par la relation suivante :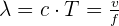 
Avec :
- λ longueur d'onde en mètre (m) ;
- c célérité en mètre par seconde (m.s-1) ;
- T période temporelle en seconde (s) ;
- f fréquence en Hertz (Hz).
La périodicité d'une onde
On parle de périodicité dans le cas d'une onde mécanique progressive. Une période est un temps qui se mesure habituellement en secondes. Elle représente le temps qui s'écoule entre deux moments identiques de l'onde.
Une fois qu'on connait la période, on peut facilement définir la fréquence de l'onde. Celle-ci est égale à l'inverse de la période.
La direction des ondes
Il existe des ondes mécaniques progressives qui se propagent suite à une perturbation dans un milieu matériel, le tout sans transport de matière mais avec un transport d'énergie.
Deux types d'ondes mécaniques progressives existent : les ondes transversales et les ondes longitudinales.
- Onde transversale : Onde pour laquelle la matière est momentanément déplacée dans une direction perpendiculaire à la direction de la propagation.
- Onde longitudinale : Onde pour laquelle la matière est momentanément déplacée dans une direction parallèle à la direction de la propagation.
Calculer une longueur d'onde
Si une onde a une vitesse de propagation "c" et une période T, alors sa longueur peut être calculée grâce à la relation suivante : 
Avec :
- λ en mètre (m) ;
- c en mètre par seconde (m.s-1) ;
- T en seconde (s).
Il est également possible de calculer la longueur d'onde lorsqu'on connait la vitesse de propagation c et la fréquence f avec la relation suivante :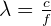 
Avec :
- λ en mètre (m) ;
- c en mètre par seconde (m.s-1) ;
- f en hertz (Hz).
Les relations précédentes impliquent :
- Que la longueur d'onde est proportionnelle à la période, ce qui signifie qu'elle est donc d'autant plus élevée que la période est grande ;
- Que la longueur d'onde est inversement proportionnelle à la fréquence, et donc qu'elle est donc d'autant plus élevée que la fréquence est faible.
Pour rappel, 
La fréquence d'une onde
Les signaux à transmettre usuellement, comme par exemple les sons (voix des pilotes, des contrôleurs aériens), sont constitués d’ondes de basses fréquences. Leur faible distance de propagation, la superposition d’un grand nombre de ces signaux dans l’environnement et le fait que les dimensions des antennes réceptrices doivent être de l’ordre de grandeur de la longueur d’onde des signaux à capter, constituent autant d’obstacles à leur utilisation directe.
La modulation est alors une solution pour transmettre les signaux : on fait varier l’une des caractéristiques (amplitude, fréquence…) d’un signal de fréquence beaucoup plus élevée (porteuse), avec l’information à transmettre (signal modulant). On obtient un signal modulé.
Le phénomène d'interférences
Une interférence est un phénomène de mécanique ondulatoire qui se produit lorsque deux ondes interagissent. Il y a interférence en un point de l'espace si deux ondes s'y superposent : en ce point les amplitudes des deux ondes s'additionnent. Exemple : interférence en un point A entre deux perturbations se propageant à surface de l'eau dans des sens opposés.
- Le point A n'est encore atteint par aucune perturbation et se trouve à son niveau initial.
- Le point A se trouve au niveau d'élévation maximale car les deux perturbations y additionnent leur amplitude maximale : on dit qu'il s'agit d'une interférence constructive.
- Le point A retrouve sont niveau initial et les deux perturbations se compensent.
- Le point A se trouve au niveau le plus bas car les deux perturbations additionnent leur amplitude minimale.
Conditions de formation des interférences
Pour obtenir des interférences stables, il est nécessaire que :
- Les ondes aient même fréquence
- Les ondes aient un déphasage constant
Les ondes sont alors dites synchrones. En pratique, ces conditions sont respectées lorsqu'une même source est à l'origine des deux ondes qui interfèrent : grâce à une réflexion ou en divisant une onde en deux faisceaux. En effet, deux sources de lumière différentes ne sont pas cohérentes. Le déphasage est donc inconstant. De plus, la fréquence des ondes émises est très élevée par rapport à ce que l’œil est capable de détecter. En effet, la lumière nous semble continue. Le déphasage est inconstant mais, surtout varie tellement rapidement que l’œil ne peut percevoir que la moyenne des déphasage. Cette moyenne étant nulle, il n'y a pas d'interférences visibles. L'intensité observée est simplement la somme des deux intensités.
Le déphasage de deux ondes sinusoïdales
Le déphasage entre deux ondes sinusoïdales en un point donné de l'espace permet de prévoir si elles interfèrent de manière constructive ou destructive. Lorsque deux ondes interférent en un point P de l'espace le déphasage Δφ entre ces dernières est donné par la relation : 
- où τ1 est le retard de la première onde au point P (en seconde)
- τ2 est le retard de la seconde onde au point P (en seconde)
- T est la période commune aux deux ondes (en seconde)
- Δφ est le déphasage (en radian)
Cas particuliers de déphasage
Si le déphasage Δφ est égale à :
- 0 alors les ondes sont dites en phase
- π : les ondes sont dites en décalage de phase
- π/2 : les ondes sont dites en quadrature de phase
Interférences constructives et destructives de deux ondes sinusoïdales
Interférences constructives
On dit qu'une interférence est constructive si elle correspond à la superposition de deux ondes ayant une amplitude maximale. Pour deux ondes lumineuses monochromatiques les interférences constructives correspondent à une intensité lumineuse maximale. Une interférence constructive est obtenue dans le cas d'un déphasage égale à un multiple pair de pi, ce qui peut se traduire par la relation suivante : [Δφ =2kpi] où k est un nombre entier
Interférences destructives
On dit qu'une interférence est destructive si elle correspond à la superposition de deux ondes ayant une valeur minimale. Pour deux ondes lumineuses monochromatiques les interférences destructives correspondent à une intensité lumineuse minimale voir nulle. Une interférence destructive est obtenue dans le cas d'un déphasage égale à un multiple impair de pi, ce qui peut se traduire par la relation suivante :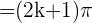 
où k est un nombre entier
Interférence de deux ondes lumineuses monochromatiques
Afin de satisfaire aux conditions de formation des interférences il est courant d'utiliser un dispositif appelé " fentes d'Young ". Il s'agit de simplement de deux fines fentes parallèles éclairées par la même lumière laser et qui jouent le rôle deux sources distinctes. Ces deux sources secondaires émettent des lumières qui interfèrent grâce au phénomène de diffraction. La figure d'interférence observée sur un écran est formée d'une alternance de franges sombres et lumineuses qui viennent s'insérer dans la figure de diffraction. 
Figure d'interférence d'interfrange i obtenue à partir des fentes d'Young éclairées par une lumière laser
L’interfrange (notée i) entre deux franges sombres est donnée par la relation suivante :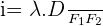 
- où i est la distance entre les centres des deux franges sombres successives (en mètre)
- λ est la longueur d'onde des deux ondes qui interfèrent (en mètre)
- F1F2 est la distance entre les deux fentes parallèles (en mètre)
- D est la distance entre les fentes et l'écran (en mètre)
Les interférences dans la vie courante
Dans l'industrie chimique
Les interférences sont très utilisés pour les appareils d'analyse optique en chimie. Par exemple l'analyseur infrarouge, volontiers appelé analyseur infrarouge à transformé de fourrier dans l'industrie du vin, en est un exemple. Il s'appelle ainsi car le spectre initialement obtenus est un interférogramme qui nécessite l'intervention de la transformé de fourrier pour obtenir le spectre de la transmittance en fonction du nombre d'onde. Cette technique permet d'analyser simultanément un large spectre de longueur d'onde et donc de pouvoir obtenir assez simplement et très rapidement un spectre infrarouge d'un échantillon.
L'holographie
Nous distinguons les objets car ceux-ci modifient la lumière qu'il reçoivent :
- la longueur d'onde : traduite par l’œil comme la couleur
- l'amplitude : traduite par l’œil comme étant l'intensité lumineuse
- le déphasage : il dépend des points de l'objet et donc de la distance à l’œil. Cela permet d'appréhender la profondeur. C'est ce même déphasage d'onde sonore qui permet d'identifier l'origine d'un son dans l'espace.
L'hologramme pourrait être comparer à la de la photographie en 3D. La photographie se "contente" d'imprimer sur un support photosensible l'intensité lumineuse et la longueur d'onde de la lumière en chaque point de l'espace pris en photo. L'hologramme prend en compte le déphasage des ondes. La création d'un hologramme nécessite d'utiliser les propriétés d'interférences et de diffraction d'un faisceau cohérent (en phase, monochromatique et directive). Le laser est alors la seule source lumineuse possible pour la création d'un support holographique. Il faut enregistrer sur une plaque photographique par exemple, l'interférogramme d'un faisceau laser divisé en deux par jeu de miroirs :
- Le premier faisceau est directement projeté sur la plaque photographique : c'est le faisceau de référence
- le deuxième éclair l'objet dont on souhaite l'hologramme puis est recueilli sur une plaque photographique. les deux faisceaux cohérent mais en déphasage (pas même chemin parcouru) interfèrent
- Sur la plaque photographique, les intensités maximum correspondent au point de l'espace ou les deux faisceaux sont en phase. L'intensité dépend également de la luminosité initiale en chaque point de l'objet.
Ensuite, il faut ré-éclairer l'hologramme enregistrée, en général avec le même laser (c'est également possible avec une lumière incohérente), ainsi l'objet est restitué avec l'impression de profondeur donnée par les différences de phase.
A noter que les concerts en hologramme de concert de Claude François ne sont pas en réalité des hologramme au sens optique du terme. Il s'agit en réalité d'un fantôme de Pepper (du nom de celui qui a popularisé la technique). Cette technique utilise en réalité simplement le reflet du chanteur sur un écran transparent au milieu de la scene, de telle sorte qu'il parait être réellement au milieu des musiciens qui eux sont réels.
Vous avez aimé cet article ? Notez-le !
Loading...
Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
excelent
1-Un exemple pour chacune des hypothèses sur les préférences du consommateur
2-une ou deux raisons qui peuvent provoquer un déplacement de la courbe d’interférence
Juste un tout petit détail dans le paragrphe « cas particuliers de déphasage » : un décalage de phase de PI, s’appelle « opposition de phase ».
« Il y a interférence en un point de l’espace si deux ondes s’y superposent : en ce point les amplitudes des deux ondes s’additionnent. »
Le phénomène d’interférence est justement caractérisé par le fait que l’amplitude résultante n’est pas la somme des deux amplitudes. L’amplitude est une grandeur strictement positive. L’intérêt des interférence est que la somme de deux ondes peut donner une onde nulle en certain point.
Ce sont les ondes qui s’additionnent, pas leurs amplitudes.
bonjour
pourquoi si on a l’interférence enter deux onde de même fréquence , l’effet dépendra des phase aussi bien que des amplitude des ondes électromagnétique
Merci!
Merci, c’est cool d’avoir de nouvelles informations.
Merci
Cool merci !
je passe le bac dans 2 mois et je suis en galere totale heureusement que je tombe surr ce site