Chapitres

L’indice du milieu
Dans un matériau transparent (c’est-à-dire sans absorption, comme l’air ou l’eau par exemple), la vitesse v de propagation de l’onde est toujours inférieure à la vitesse de propagation de l’onde dans le vide c.
On peut caractériser un matériau par le rapport c/v, qui donne l’indice n.

L’indice n d’un matériau est un nombre sans dimension, toujours supérieur à 1. Cela s’explique par la relation suivante :
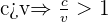
Voici les indices des milieux les plus courants :
| Milieu | Indice n du milieu | % vitesse de propagation par rapport à c |
|---|---|---|
| Vide | 1.00000 | 100% |
| Air | 1.00029 | 99.97% |
| Eau | 1.33 | 75% |
| Verre | 1.5 à 1.7 | 59% à 67% |
| Diamant | 2.42 | 41% |
Un dioptre est l’ensemble constitué par deux milieux transparents d’indice différent, ainsi que leur interface. C’est cette interface qui détermine la géométrie du dioptre.
On dit d’un milieu transparent qu’il est plus réfringent qu’un autre milieu transparent lorsque son indice de réfraction est plus élevé que celui de l’autre milieu. La réfringence est la capacité d’un milieu à réfracter la lumière. L’indice de réfraction est une mesure de la réfringence d’un milieu pour une lumière de fréquence donnée.
Généralités sur les lois de Snell-Descartes
Les lois de Snell-Descartes découlent du principe de Fermat, qui postule que la lumière qui se propage en ligne droite dans un milieu homogène prend le chemin le plus rapide pour aller d’un point à un autre. Ce chemin ne dépend pas du sens du parcours.
La première loi de Snell-Descartes : loi du plan d’incidence
Cette loi indique dans quel plan se trouve le rayon lumineux réfracté : le rayon réfracté appartient au même plan que la normale et le rayon incident.

La deuxième loi de Snell-Descartes : loi de la réflexion
Notion de réflexion
Lorsque la lumière atteint la surface d’un dioptre, une partie de la lumière est réfractée (donc déviée dans le nouveau milieu) alors que l’autre partie est renvoyée dans le milieu d’origine : ces rayons subissent une réflexion.
La loi de la réflexion
Les rayons incident et réfléchi font un angle égal et opposé avec la normale à la surface du dioptre :

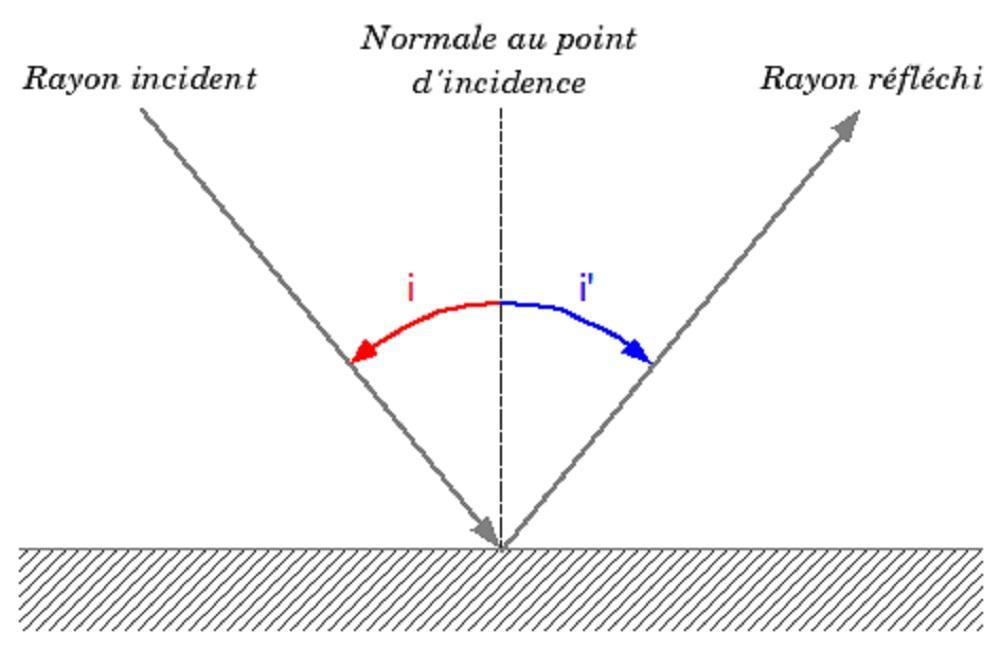
Réflexion totale
Si le milieu 2 est moins réfringent que le milieu 1, c’est-à-dire n1>n2, il existe un angle critique (ilim). La limite sin i = n2/n1 définit un angle limite ilim = arcsin (n2/n1), au-delà duquel il n’y a plus de rayon réfracté. Toute la lumière est alors réfléchie dans le premier milieu. Il y a réflexion totale pour i > ilim.
Applications
Cette propriété peut être utilisée pour transmettre sans perte, ou presque, une onde électromagnétique dans une fibre.
Le principe de la réflexion totale permet par exemple de guider la lumière dans un conduit d’indice supérieur à celui du milieu environnant.
Ici, la réflexion totale permet la propagation de la lumière par réflexions totales successives à l’interface conduit-milieu extérieur.
La fibre optique peut être utilisée dans de nombreux domaines différents comme les télécommunications ou le réseau informatique, mais également dans la médecine (afin d’éclairer des zones difficilement accessibles.
La 3e loi de Snell-Descartes : loi de la réfraction
Notion de réfraction
Lorsque la lumière passe d’un milieu d’indice n1 à un milieu d’indice n2 par un dioptre, une partie de la lumière continue de se propager dans le milieu d’indice n2 en subissant une déviation : c’est ce que l’on appelle une réfraction.
Loi de la réfraction
Les rayons incidents issus d’un milieu d’indice n1 et réfracté dans un milieu d’indice n2 forment des angles, respectivement i et r, avec la normale à la surface. Ces angles sont liés par la relation :
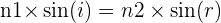

Prévoir le sens de déviation d'un rayon réfracté
La loi implique également la relation suivante entre les angles d’incidente i et de réfraction r :

- Si le premier milieu est plus réfringent que le deuxième, c'est à dire si n1>n2 cela signifie que le rapport des indices est supérieur à 1 et donc r > i : le rayon réfracté s'éloigne de la normale.
- Si le deuxième milieu est plus réfringent que le premier, c'est à dire si n2>n1 cela signifie que le rapport des indices est inférieur à 1 et donc r < i : le rayon réfracté se rapproche de la normale
Lorsque la valeur de sin (r) est connue il suffit d'utiliser, sur une calculatrice, la fonction inverse du sinus (souvent notée sin-1). Selon les paramètres utilisés la calculatrice indique l'angle de réfraction en degré ou en radian.
Applications de la réfraction
Le prisme et le principe de l’arc en ciel
Un prisme est un solide possédant des faces triangulaires, composé d’un milieu transparent limité par deux dioptres non parallèles entre eux. Ces propriétés de dispersion et de déviation de la lumière permettent de décomposer la lumière blanche.
En effet, en projetant de la lumière blanche à travers un prisme, il est possible d’observer toutes les radiations du visible. Cela est dû à la relation entre l’indice de réfraction du milieu et la longueur d’onde de la radiation lumineuse : plus la longueur d’onde est grande, plus n sera faible. Or plus n est faible, moins le rayon est dévié : cela explique que les rayons rouge sont moins déviés que les rayons bleus. La dispersion des rayons est donc due à la variation de l’indice de réfraction en fonction de la longueur d’onde.
Les arcs-en-ciel se forment d’une façon similaire. Lorsque que le Soleil traverse des gouttelettes de pluie, les rayons du Soleil font se réfracter et disperser les différentes radiations qui les composent. Ces radiations vont se réfléchir sur le fond de la goutte d’eau, puis subir une seconde réfraction en sortant de la goutte d’eau, ce qui aura pour effet d’accentuer les couleurs.
Les mirages
Les mirages sont des illusions d’optique dues à la déviation des rayons lumineux par des superpositions de couches d’air de températures différentes.

En effet, l’indice de réfraction de l’air augmente lorsque la température diminue. Cela peut provoquer une courbure des rayons lumineux.
Ainsi, si l’air situé à proximité du sol est plus chaud que celui situé en altitude, les rayons lumineux venant du ciel vont se courber vers le haut : c’est ce que l’on appelle un mirage chaud, qui peut donner l’illusion d’apercevoir de l’eau.
Au contraire, si l’air situé à proximité du sol est plus froid, les rayons venant du sol vont se courber vers le bas, donnant ainsi un mirage froid.
Pour plus d'informations, voir aussi :
- cours "Réflexion et réfraction de la lumière"
- cours "Indice de réfraction et dispersion"
- fiche "La réfraction"
- fiche "vérification expérimentale de la loi de la réfraction"























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Salut.
J’ai un soucis concernant la loi de Kepler car je n’arrive pas à faire le lien entre l’angle d’incidence et cette lois de Kepler sur la réfraction.
Merci de m’avoir accordé ce document qui m’a permis de retenir certaines notions
Je suis étudiants et je veux comprendre la physique merci mon chef scientifique
Salut je voudrais connaître toute les notion qui interviennent dans les *condition de faible incidence* svp svp svp
Salut moi je n’arrive pas à comprendre comment l’indice de réfraction peut affecté la longueur d’onde. une démonstration par formule suffira largement.
Salut, j’aimerais savoir la notion de
réflexion ou de réfraction sur les petits angles
Bonjour, avez-vous essayé de contacter l’un de nos professeurs pour recevoir une aide personnalisée ? Excellente journée ! 🙂